本文发布于61 天前,其中的信息可能已经过时,如有错误请发送邮件到supper@vcclient.xyz
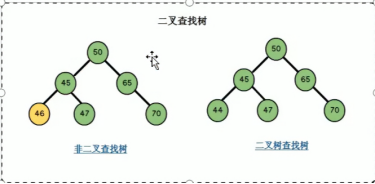
二叉査找树英文缩写为BST树(Binary Search Tree),一般也被称为二叉搜索树或者二叉排序树,二叉查找树的结点是有键值key的,如果二叉査找树不是空树则需要遵循以下的特点:
- 如果二叉査找树有左子树,则左子树的结点的键值key要小于左子树的根结点的键值key
- 如果二叉查找树有右子树,则右子树的结点的键值key要大于右子树的根结点的键值key
- 对于二叉查找树而言,左子树和右子树也分别是二叉查找树。
/******************************************************************************
*
* file name : BST二叉查找树
* author : Wzy
* data : 2025/12/11
* function : 设计BST二叉查找树的接口,为了方便对二叉树进行节点的增删,所以采用双向不循环链表来实现,每个节点的内部都需要有两个指针,分别指向该节点的左子树(lchild)和右子树(rchild)
* note : 实现了向BST二叉查找树中插入新结点,以及BST二叉查找树的前序遍历、中序遍历、后续遍历、二叉树的所有的结点树、二叉树的所有的叶子结点树、二叉树的深度
*
* copyRight (c) 2025 17630246607@163.com All Right Reseverd
* ****************************************************************************/
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#include "drawtree.h"
#if 0
//指的是BST树中的节点有效键值的数据类型,用户可以根据需要进行修改
typedef int DataType_t;
//构造BST树结点,BST树中所有结点的数据类型应该是相同的,每个结点有三部分组成,第一部分是节点的键值,第二部分是左子树的指针域,第三部分是右子树的指针域
typedef struct BSTreeNode
{
DataType_t data; //节点的键值
struct BSTreeNode *lchild; //左子树的指针域
struct BSTreeNode *rchild; //右子树的指针域
}BSTnode_t;
#endif
/******************************************************************************
*
* func name : BSTree_Create
* function : 创建一个带根节点的BST树,对BST树的根结点进行初始化
* argument : None
* retval : 返回头结点地址
* author : Wzy
* date : 2025/12/11
* note : None
*
* ****************************************************************************/
//创建一个带根节点的BST树,对BST树的根结点进行初始化
BSTnode_t* BSTree_Create(DataType_t data)
{
//1.创建一个根节点并对根结点申请内存
BSTnode_t *Root = (BSTnode_t *)calloc(1,sizeof(BSTnode_t));
if(NULL == Root)
{
perror("calloc memory for Root is failed");
exit(-1); //程序异常终止
}
//2.对根结点进行初始化,根结点的2个指针域分别指向NULL
Root->data = data;
Root->lchild = NULL;
Root->rchild = NULL;
//3.把根结点的地址返回
return Root;
}
/******************************************************************************
*
* func name : BSTree_NewNode
* function : 创建新的结点,并对新结点进行初始化(键值+左子树的地址+右子树的地址)
* argument :
* @DataType_t data:结点的键值,即自身要存储的数据
* retval : 返回新结点的地址
* author : Wzy
* date : 2025/12/11
* note : None
*
* ****************************************************************************/
//创建新的结点,并对新结点进行初始化(键值+左子树的地址+右子树的地址)
BSTnode_t * BSTree_NewNode(DataType_t data)
{
//1.创建一个新的结点并对新结点申请内存
BSTnode_t *New = (BSTnode_t *)calloc(1,sizeof(BSTnode_t));
if(NULL == New)
{
perror("calloc memory for NewNode is failed");
return NULL;
}
//2.对新结点的数据域和指针域进行初始化。
New->data = data;
New->lchild = NULL;
New->rchild = NULL;
return New;
}
/******************************************************************************
*
* func name : BSTree_InsertNode
* function : 在一个BST二叉查找树中插一个新的结点
* argument :
* @ Root: 一个指向根结点的指针。
* @DataType_t data:结点的键值,即自身要存储的数据
* retval : 成功插入返回true,插入失败返回false
* author : Wzy
* date : 2025/12/11
* note : 规则:根节点的左子树的键值都是比根节点的键值小的,根节点的右子树的键值都是比根节点的键值大的
*
* ****************************************************************************/
//向BST树中加入新结点
bool BSTree_InsertNode(BSTnode_t *Root,DataType_t data)
{
//为了避免根节点地址丢失,所以需要对根节点地址进行备份
BSTnode_t *Proot = Root;
//1.调用BSTree_NewNode这个函数创建新节点,并且对新节点进行初始化
BSTnode_t * New = BSTree_NewNode(data);
if (NULL == New)
{
printf("Create NewNode Error\n");
return false;
}
//2.此时分析当前的BST树是否为空树,有两种情况(空树 or 非空树)
if (NULL == Root)
{
//此时BST树为空树,则直接把新节点作为BST树的根节点
Root = New;
}
//此时新节点的键值不等于根节点的键值,则需要遍历BST树,分为两种情况:键值大于根节点的键值 or 键值小于根节点的键值
else
{
while(Proot)
{
//新节点的键值和根节点的键值比较,如果相等则终止函数
if (data == Proot->data)
{
printf("Can Not Insert :New->data == Proot->data \n");
return false;
}
//新节点的键值和根节点的键值比较,如果不相等则继续分析
else
{
//新节点的键值小于根节点的键值,则把根节点的左子树作为新的根
if (data < Proot->data)
{
if (Proot->lchild == NULL)
{
Proot->lchild = New;
break;
}
Proot = Proot->lchild;
}
else
{
if (Proot->rchild == NULL)
{
Proot->rchild = New;
break;
}
Proot = Proot->rchild;
}
}
}
}
return true;
}
/******************************************************************************
*
* func name : BSTree_PreOrder
* function : 前序遍历二叉树
* argument :
* @ Root: 一个指向根结点的指针。
* retval : 成功遍历返回true,遍历失败返回false
* author : Wzy
* date : 2025/12/11
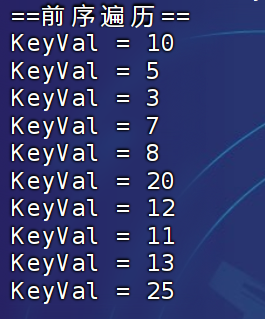
* note : 规则:前序遍历(根结点-->左子树-->右子树),体现“递归”
*
* ****************************************************************************/
//前序遍历
bool BSTree_PreOrder(BSTnode_t *Root)
{
//使用递归函数,必须提前写好终止条件
if(NULL == Root)
{
return false;
}
//先输出根节点的键值
printf("KeyVal = %d\n",Root->data);
//在输出根节点的左子树
BSTree_PreOrder(Root->lchild);
//在输出根节点的右子树
BSTree_PreOrder(Root->rchild);
return true;
}
/******************************************************************************
*
* func name : BSTree_InOrder
* function : 中序遍历二叉树
* argument :
* @ Root: 一个指向根结点的指针。
* retval : 成功遍历返回true,遍历失败返回false
* author : Wzy
* date : 2025/12/11
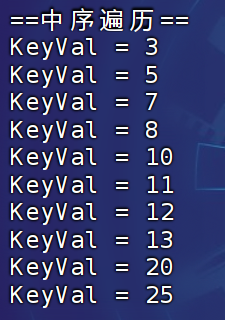
* note : 规则:中序遍历(左子树-->根结点-->右子树)
*
* ****************************************************************************/
bool BSTree_InOrder(BSTnode_t *Root)
{
//使用递归函数,必须提前写好终止条件
if(NULL == Root)
{
return false;
}
//先输出根节点的左子树
BSTree_InOrder(Root->lchild);
//在输出根节点的键值
printf("KeyVal = %d\n",Root->data);
//在输出根节点的右子树
BSTree_InOrder(Root->rchild);
return true;
}
/******************************************************************************
*
* func name : BSTree_PostOrder
* function : 后序遍历二叉树
* argument :
* @ Root: 一个指向根结点的指针。
* retval : 成功遍历返回true,遍历失败返回false
* author : Wzy
* date : 2025/12/11
* note : 规则:后序遍历(左子树-->右子树-->根结点)
*
* ****************************************************************************/
bool BSTree_PostOrder(BSTnode_t *Root)
{
//使用递归函数,必须提前写好终止条件
if(NULL == Root)
{
return false;
}
//在输出根节点的左子树
BSTree_PostOrder(Root->lchild);
//在输出根节点的右子树
BSTree_PostOrder(Root->rchild);
//先输出根节点的键值
printf("KeyVal = %d\n",Root->data);
return true;
}
/******************************************************************************
*
* func name : BinaryTree_CountNode
* function : 计算一颗给定二叉树的所有结点数
* argument :
* @ Root: 一个指向根结点的指针。
* retval : n1+n2+1:n1用来计算左子树的节点,n2用来计算右子树的节点,返回二叉树的所有结点数
* author : Wzy
* date : 2025/12/11
* note : 总结点数 =左子树的结点数 + 右子树的结点数 +1 采用递归实现
*
* ****************************************************************************/
int BinaryTree_CountNode(BSTnode_t *Root)
{
int n1,n2; //n1用来计算左子树的节点,n2用来计算右子树的节点
//使用递归函数,必须提前写好终止条件
if(NULL == Root)
{
return 0;
}
//假设采用后序遍历来计算二叉数的节点数量
n1 = BinaryTree_CountNode(Root->lchild);
n2 = BinaryTree_CountNode(Root->rchild);
return n1+n2+1;
}
/******************************************************************************
*
* func name : BinaryTree_CountLeafNode
* function : 计算一颗给定二叉树的所有的叶子节点数量
* argument :
* @ Root: 一个指向根结点的指针。
* retval : 如果是空树,直接返回0,如果只有一个根节点,则根节点就是叶子节点,返回1,
* 说明这是有子树的二叉树,则需要计算左子树的叶子节点和右子树的叶子节点,返回n1+n2,n1用来计算左子树的叶子节点,n2用来计算右子树的叶子节点
* author : Wzy
* date : 2025/12/12
* note : 总的叶子结点数 =左子树的叶子结点数 + 右子树的叶子结点数 +1 采用递归实现
*
* ****************************************************************************/
int BinaryTree_CountLeafNode(BSTnode_t *Root)
{
int n1,n2; //n1用来计算左子树的叶子节点,n2用来计算右子树的叶子节点
//使用递归函数,必须提前写好终止条件
if(NULL == Root)
{
//说明是空树,直接返回0
return 0;
}
else if (Root->lchild == NULL && Root->rchild == NULL)
{
//说明只有一个根节点,则根节点就是叶子节点
return 1;
}
else
{
//说明这是有子树的二叉树,则需要计算左子树的叶子节点和右子树的叶子节点
n1 = BinaryTree_CountLeafNode(Root->lchild);
n2 = BinaryTree_CountLeafNode(Root->rchild);
return n1+n2;
}
}
/******************************************************************************
*
* func name : BinaryTree_GetDepth
* function : 计算一颗给定二叉树的深度
* argument :
* @ Root: 一个指向根结点的指针。
* retval : 如果是空树,直接返回0,如果只有一个根节点,则根节点就是叶子节点,返回1,
* 说明这是有子树的二叉树,则需要计算左子树的深度和右子树的深度,返回n1+n2,n1用来计算左子树的深度,n2用来计算右子树的深度
* author : Wzy
* date : 2025/12/12
* note : 二叉树的深度= ( max(左子树的深度,右子树的深度) ) + 1
*
* ****************************************************************************/
int BinaryTree_GetDepth(BSTnode_t *Root)
{
int n1,n2; //n1用来计算左子树的深度,n2用来计算右子树的深度
//使用递归函数,必须提前写好终止条件
if(NULL == Root)
{
//说明是空树,直接返回0
return 0;
}
else if (Root->lchild == NULL && Root->rchild == NULL)
{
//说明只有一个根节点,则二叉树的深度为1
return 1;
}
else
{
//说明这是有子树的二叉树,则需要计算左子树的深度和右子树的深度
n1 = BinaryTree_GetDepth(Root->lchild);
n2 = BinaryTree_GetDepth(Root->rchild);
}
return ((n1 > n2) ? n1 : n2) + 1;
}
int main(int argc, char const *argv[])
{
int Node; //用于记录二叉树的节点数
int LeafNode;//用于记录二叉树的叶子节点数
int Depth; //用于记录二叉树的深度
//1.创建一个带根节点的BST树
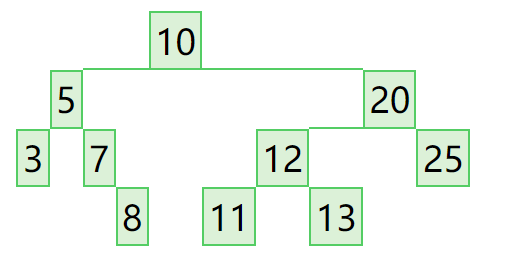
BSTnode_t* root = BSTree_Create(10); //此时根节点的键值为10
//2.向BST树中插入新节点
BSTree_InsertNode(root,5);
BSTree_InsertNode(root,20);
BSTree_InsertNode(root,7);
BSTree_InsertNode(root,12);
BSTree_InsertNode(root,8);
BSTree_InsertNode(root,3);
BSTree_InsertNode(root,25);
BSTree_InsertNode(root,11);
BSTree_InsertNode(root,13);
draw(root); //调用一个库函数,画出这个BST二叉查找树
printf("==前序遍历==\n");
BSTree_PreOrder(root);
printf("\n");
printf("==中序遍历==\n");
BSTree_InOrder(root);
printf("\n");
printf("==后序遍历==\n");
BSTree_PostOrder(root);
printf("\n");
printf("==二叉树的所有结点数==\n");
printf("Node = %d\n",Node = BinaryTree_CountNode(root));
printf("\n");
printf("==二叉树的所有叶子结点数==\n");
printf("LeafNode = %d\n",LeafNode = BinaryTree_CountLeafNode(root));
printf("\n");
printf("==二叉树的深度==\n");
printf("Depth = %d\n",Depth = BinaryTree_GetDepth(root));
printf("\n");
return 0;
}
测试结果